Mesa Optimizers and Language Recursion

Scaling laws are one big unsolved problem in machine learning, and especially NLP. NLP hits the sweet spot where the problems are hard enough to still require ongoing research, but problems are also easy enough to have real practical applications, so the field continues to get funded. One problem some people have raised is the idea of a "mesa optimizer", or a model that has learned a generic way of solving a task that may not be directly what you expect. For example, a computer that plays Chess may eventually figure out how to do heuristic tree-pruning. Originally I was pretty against this idea, it seems somewhat silly, and there's no real proof that we'll ever develop anything that produces a mesa optimizer. However, I've become more of a mesa optimizer truther with time, the more I read about linguistics, the more likely I think mesa optimizers are going to end up.

I was reading a paper by Hauser, Chomsky, and Finch on how to approach the study of linguistics, and they distinguish between what they call an FLN and a FLB, or a faculty of language narrow, and a faculty of language broad. In short, they define FLN to be centered around the idea of recursion, that the discovery of recursion is the key distinguishing feature for human languages vs animal languages. They provide the example that human babies can infer the existence of "4" after learning 1, 2, and 3, but primates require learning each one individually. They've got this diagram to show:

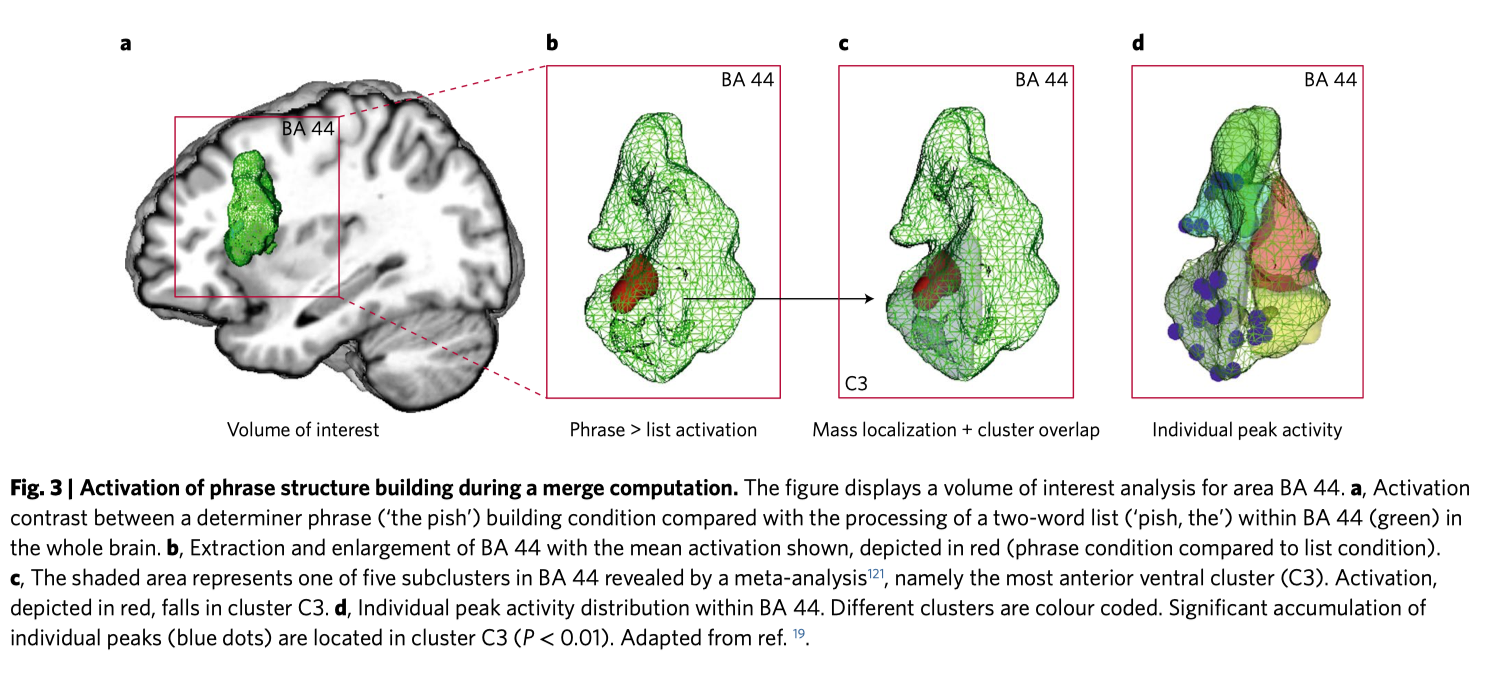
This is all fine, we can easily construct sentences that require recursion (the sentence "Mary said that Jane said that Tom said…"). Zaccarella and Friederici talk about how they’ve identified a single area of the brain that performs the "merge operation", where you can convert “the" and “fish" into a single linguistic unit if "the fish" but not “fish” and “the”. Friederici identifies that Broca’s Area 44, near the center of your brain, lights up when it needs to perform this operation:

If we accept that merge operations are necessary for recursion, since you need to be able to merge parts after finishing recursion, we can then believe that recursion has some biological basis.

But what does recursion allow us to get away with? If we can infer the existence of 4 from knowing 1, 2, and 3, and we can also infer the existence of 5 from knowing 1-4, and so on, what does this actually get us? Here, recursion offers a compression, rather than learning every single number individually, recursion lets us compress numbers down to the n+1 rule. If we know that every number bigger than n can eventually be derived from performing n+1 some arbitrary amount of times, there’s no need to memorize every larger number. Similarly, with some basic units (verbs, adjectives, nouns, etc) and a simple set of rules (subject comes before verb, object comes after verb, etc) we can construct English sentences. There’s no need to memorize all (or even most) of the English sentences in existence, you can simply rederive them with a set of rules.

To use an analogy, this would be similar to printing every possible path from your home to work, versus learning how to read a compass and learning which directions the roads go. You could certainly list every single combination of roads that take you to work (I can start on A road and then go to B, or I can start on C road and go to B to connect with D…), or you could simply learn that your work is southeast of your home, and that roads generally go north/south between the two places.

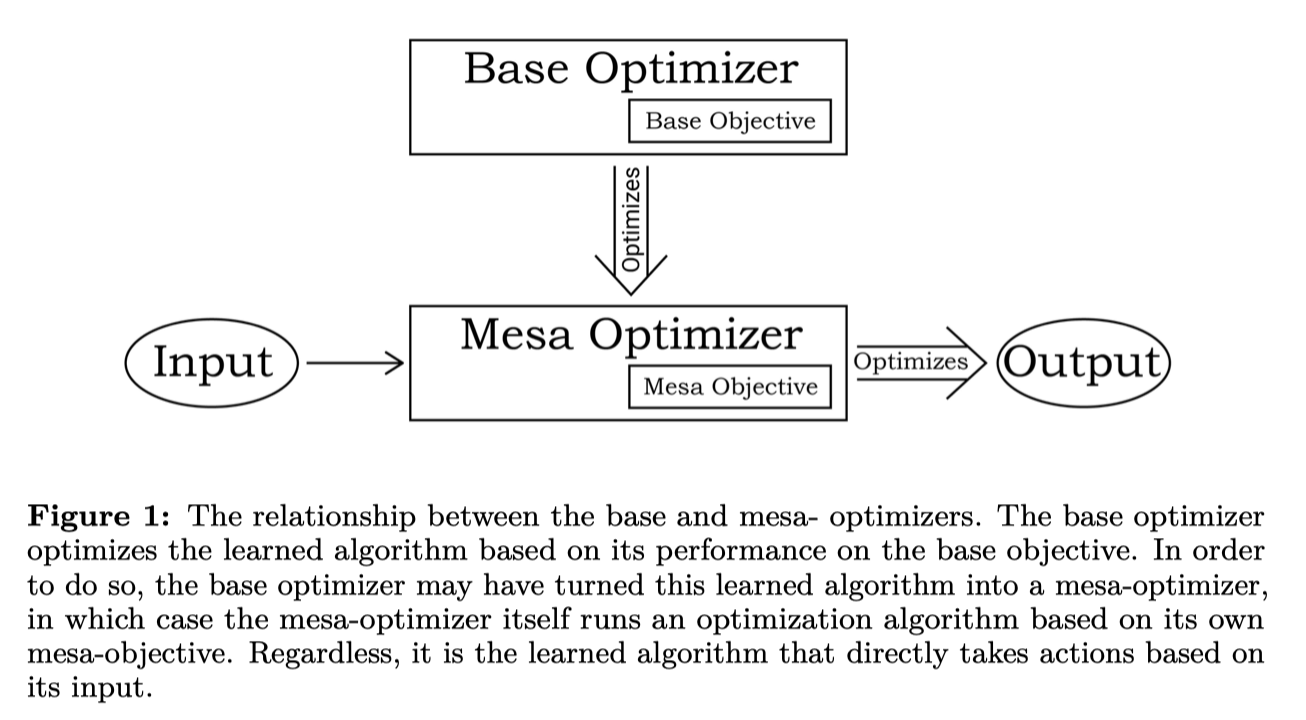
Hubinger et al wrote about the theoretical concept of a "mesa optimizer". This is the concept that if you teach a model to do something, and subject it to intense evolutionary pressure, you can end up with what’s known as a "mesa optimizer". One example given in the paper is teaching models to play Chess/Shogi/Go, where after enough iterations, the model may simply develop a heuristic tree pruning algorithm. In another example, we could think about solving a maze: you start off with the model learning to explore every possible maze path, but eventually it could develop a generic path-finding algorithm like A*. In these two cases, the heuristic tree-pruning algorithm and A* are both "mesa optimizers". In other words: the regular optimizer (such as stochastic gradient descent) develops the mesa optimizer:

One thing that Hubinger et al identify is that mesa optimizers are "compressible", or that they take up less memory space (described as bits) and less computation than other options. For example, in Chess, it would take a lot of memory space and computational time to list out every single possible game state. It would be much more efficient space-wise to develop a generic algorithm, such as heuristic tree-pruning, rather than figure out every single situation.

This is the connection between mesa optimizers and linguistic recursion: both are compressed forms of the greater problem. Mesa optimizers are context dependent, rather than figuring out every possible situation beforehand, mesa optimizers use the current information around the game state to figure out the next move. For language, Chomsky developed the idea of context-free and context-sensitive grammars, English words change meaning and form based on the words around it. Yet we’re able to understand the potentially infinite set of English sentences despite only learning a very small percentage, simply because we’ve learned the rules. The recursive nature of English allows us to learn some basic rules and generate and understand far more than what we’ve experienced.

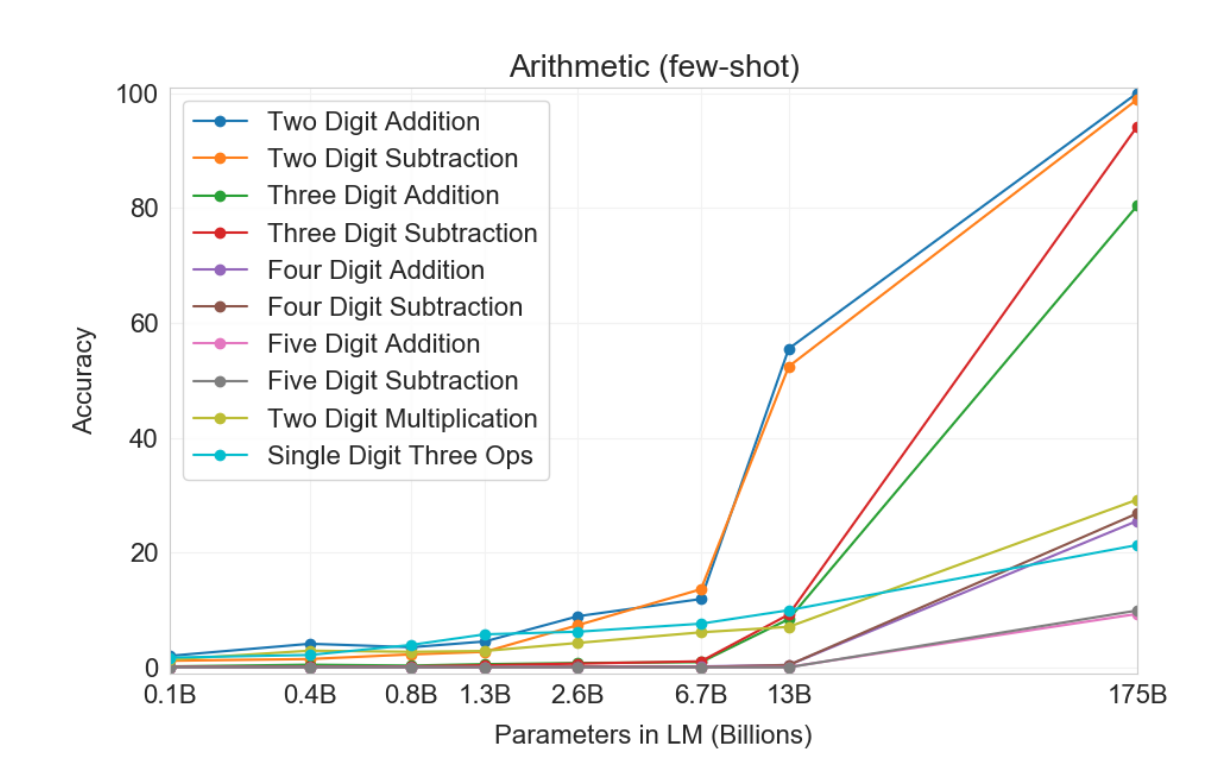
So if it follows that mesa optimizers and languages are similar in that they both capture more efficient forms of a problem, what does this idea do for us? For one, mesa optimizers are purely theoretical (although Deepmind has claimed they developed a proto-one), but language recursion is not. Language recursion via the merge operation has taken a particular role within a small part of our brain, which presents another quandary: if language recursion via the merge operation is such a key component, why would it, evolutionarily speaking, be bottlenecked to a single portion of the brain? To me, I see this as we’re in the early stages of evolution building specific components for recursion: our brains have not fully evolved to the point where multiple parts can perform the merge operation. But despite that, we’ve been able to do a lot with only a single portion! For Chomsky, this is a major evolutionary leap, not an iterative one. We did not slowly get to recursion, but rather we managed to develop it, and suddenly the modes of communication dramatically multiplied. Speculatively speaking, this means that, if mesa optimizers were to develop, their evolution would not be iterative, I would expect a mesa optimizer to emerge out of the blue at some point, once we’ve reached neural networks with sufficient dataset size, or computational capability, just as GPT-3 does not demonstrate the ability to do single digit arithmetic until 1B parameters, but the jump is quite dramatic (from https://arxiv.org/abs/2005.14165):

I’m not sure where this leaves my thinking on this, I started out totally rejecting the idea of mesa optimizers, but as I read more about linguistics and the conundrum that linguists have in trying to figure out how language emerged, I’m beginning to be more open to the idea that mesa optimizers could also emerge out of the blue.